Exploring Knuth's multiplicative hash

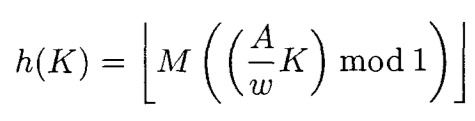
While researching some cryptography methods, I stumbled upon Knuth's multiplicative hash method. I was surprised how well it worked for how simple it is. It's not perfect but it is good enough for a lot of things you would need a hash for.

The main principal behind it is that you can make well distributed, random numbers out of an integer if you take a enough large prime number and multiply the integer by it. In the following example, I used 2,654,435,761 (0x9E3779B1) and show is it is evenly distributed for the first 100,000 integers. If you needed to hash larger numbers, you can simply use a larger prime number.

I also explored what happens when you use non-prime numbers. I knocked a few digits off the prime number earlier and used 26,544 and something interesting happened. All of the numbers clustered around the 8th element. This happens to be a factor of 26,544. You can see how having a number without factors is important in making this hash function well distributed.